#include <GalerkinStepInternals.hpp>
Public Member Functions | |
| GalerkinStepInternals (Abstract::Problem< T_M, T_Q > &problem, int quad_deg) | |
| void | setData (T_M h, T_Q q0, T_Q q1) |
| const NOXVector< T_Q::DOF *T_N_STEPS > | getInitialGuess () |
| const NOXVector< T_Q::DOF *(T_N_STEPS-1)> | initGetInitialGuess () |
| void | updatePosition (const NOXVector< T_Q::DOF *T_N_STEPS > &q) |
| void | updateInitialPosition (const NOXVector< T_Q::DOF *(T_N_STEPS-1)> &q) |
| bool | computeF (NOXVector< T_Q::DOF *T_N_STEPS > &f, const NOXVector< T_Q::DOF *T_N_STEPS > &q) |
| bool | computeInitF (NOXVector< T_Q::DOF *(T_N_STEPS-1)> &f, const NOXVector< T_Q::DOF *(T_N_STEPS-1)> &q) |
| bool | computeJacobian (Eigen::Matrix< double, T_Q::DOF *T_N_STEPS, T_Q::DOF *T_N_STEPS > &J, const NOXVector< T_Q::DOF *T_N_STEPS > &q) |
| bool | computeInitJacobian (Eigen::Matrix< double, T_Q::DOF *(T_N_STEPS-1), T_Q::DOF *(T_N_STEPS-1)> &J, const NOXVector< T_Q::DOF *(T_N_STEPS-1)> &q) |
 Public Member Functions inherited from Variational::Abstract::StepInternals< T_M, T_Q, T_TQ > | |
| StepInternals (T_TQ &problem) | |
| void | setData (T_M h, T_Q q0, T_Q q1) |
| T_M | h () const |
| T_Q | q0 () const |
| T_Q | q1 () const |
| virtual T_Q | posFromVel (T_M h, T_Q q0, T_Q v0) const=0 |
| Public Member Functions inherited from Abstract::NOXStep< T_Q, T_N_STEPS > | |
| virtual bool | computeF (NOXVector< T_Q::DOF *T_N_EQUATIONS > &f, const NOXVector< T_Q::DOF *T_N_EQUATIONS > &x)=0 |
| virtual bool | computeJacobian (Eigen::Matrix< double, T_Q::DOF *T_N_EQUATIONS, T_Q::DOF *T_N_EQUATIONS > &J, const NOXVector< T_Q::DOF *T_N_EQUATIONS > &x)=0 |
Protected Attributes | |
| std::vector< T_Q > | m_v_cur_q |
| std::vector< T_Q > | m_v_prev_q |
| LagrangeInterpolation< T_Q > | m_interp |
| int | m_quad_deg |
| Protected Attributes inherited from Variational::Abstract::StepInternals< T_M, T_Q, T_TQ > | |
| T_M | m_h |
| T_Q | m_q0 |
| T_Q | m_q1 |
| T_TQ & | m_problem |
Detailed Description
template<typename T_M, typename T_Q, typename T_TQ, int T_N_STEPS>
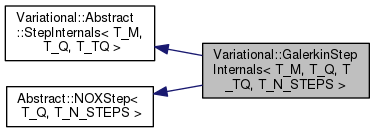
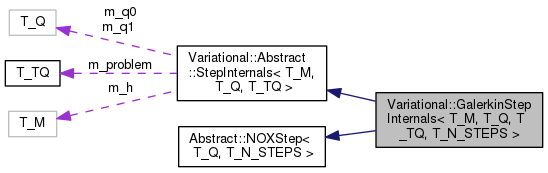
class Variational::GalerkinStepInternals< T_M, T_Q, T_TQ, T_N_STEPS >
Cette implémentation est un peu touffue, alors tâchons d'être méthodique.
Le nombre de points de contrôle est désigné par \(S+1\) dans les formules mathématiques. Dans le code, \(S\) est donné par T_N_STEPS. L'indice associé est \(\nu\in\{0,\ldots,S\}\) ou \(\mu\). Les points de contrôle sont les configurations \(q^\nu\in Q\) où l'espace \(Q\) possède T_Q::DOF degrés de liberté dénoté dans les formules par \(N\). L'ensemble des configurations associés à un pas de temps donné sont résumés par la "super"-configuration \(\bar q\) de T_Q::DOF*(T_N_STEPS+1) degrés de liberté. Il est représenté en mémoire par un std::vector<T_Q> et \(q_\nu\) est accédé par bar_q[nu].
Les polynômes de Lagrange \(\phi_\nu\) associés aux points de contrôle \(q^\nu\) sont de degré \(S\) et définis pour \(\alpha\in[0,1]\) par
\[ \phi_\nu(\alpha)=\prod_{0\leq\mu\leq S,\;\mu\neq\nu} \frac{\alpha-\alpha_\mu}{\alpha_\nu-\alpha_\mu}. \]
La courbe interpolée \(q_d\) et sa dérivée \(\dot q_d\) sont données en \(t\in[0,h]\) respectivement par
\[ q_d(t;\bar q) = \sum_{0\leq\nu\leq S} q^\nu\phi_\nu(t/h), \qquad \dot q_d(t;\bar q)=\frac{1}{h} \sum_{0\leq\nu\leq S} q^\nu\dot\phi_\nu(t/h). \]
Soit une quadrature \((c_k,w_k)\) d'ordre \(r\) parcourue par l'indice \(k\in\{0,\ldots,r-1\}\). L'action est donnée pour \(\bar q\) par
\[ \mathcal A_d(\bar q) = h\sum_{0\leq k<r}w_k L(c_kh;\bar q) \]
où \(L(c_kh;\bar q) = L(q_d(c_kh;\bar q),\dot q_d(c_kh;\bar q))\) est un raccourci de notation.
On note \(F\) la fonction que l'on cherche à annuler. Elle prend en argument les \(S\) configurations \(q_1,\ldots,q_S\) et retourne \(S\) systèmes de \(N\) équations. Le premier système d'équations correspond à la DEL et les \(S-1\) suivants aux conditions internes d'extrémalisation. On notera l'ensemble des configurations \(q_1,\ldots,q_S\) par \(\bar q^*\), c'est à dire \(\bar q\) sans la configuration \( q_0\), et
\[ F(\bar q^*)=\begin{pmatrix}F_0(\bar q^*)\\ \vdots \\ F_{S-1}(\bar q^*)\end{pmatrix} \]
où chaque \(F_i(\bar q^*)\) est un vecteur colonne de taille \(N\).
Soit \(\bar q_{n-1}\) et \(\bar q_n\) les ensembles de configurations de deux pas de temps consécutifs, la DEL est donnée par
\[ F_0(\bar q_n^*) = \sum_{0\leq k<r}w_k\left(h\left( \phi_0(c_k)\frac{\partial L}{\partial q}(c_kh;\bar q_n) +\phi_s(c_k)\frac{\partial L}{\partial q}(c_kh;\bar q_{n-1})\right) +\left(\dot\phi_0(c_k)\frac{\partial L}{\partial\dot q}(c_kh;\bar q_n) +\dot \phi_s(c_k)\frac{\partial L}{\partial\dot q}(c_kh;\bar q_{n-1}) \right)\right) = 0 \]
et les conditions internes d'extrémalisation d'action sont données pour tout \(\nu\in\{1,\ldots,S-1\}\) par
\[ F_\nu(\bar q_n^*)=\sum_{0\leq k<r}w_k\left(h\phi_\nu(c_k) \frac{\partial L}{\partial q}(c_kh;\bar q_n)+\dot\phi_\nu(c_k) \frac{\partial L}{\partial \dot q}(c_kh;\bar q_n)\right)=0. \]
Le jacobien de \(F\) est donné par
\[ J(\bar q^*)=\left(\frac{\partial F_i}{\partial q_{j+1}} (\bar q^*)\right)_{ij}. \]
Pour \(0\leq i\leq S-1\), \(1\leq j\leq S\), et \(\bar q=\bar q_n\), on calcule
\[ \frac{\partial F_i}{\partial q_j}(\bar q^*_n) = \sum_{0\leq k<r}w_k\left(\phi_i(c_k)\left(h\phi_j(c_k) \frac{\partial}{\partial q}\frac{\partial L}{\partial q} +\dot\phi_j(c_k)\frac{\partial}{\partial v} \frac{\partial L}{\partial q}\right) +\dot\phi_i(c_k)\left(\phi_j(c_k) \frac{\partial}{\partial q}\frac{\partial L}{\partial v} +\frac{1}{h}\dot\phi_j(c_k) \frac{\partial}{\partial v}\frac{\partial L}{\partial v} \right)\right) \]
où toutes les dérivées partielles du lagrangien sont prises en \((c_kh;\bar q_n)\). On vérifie en particulier que la différentielle de la DEL est donnée par
\[ \frac{\partial F_0}{\partial q_j}(\bar q^*) = \sum_{0\leq k<r}w_k\left(\phi_0(c_k)\left(h\phi_j(c_k) \frac{\partial}{\partial q}\frac{\partial L}{\partial q} +\dot\phi_j(c_k)\frac{\partial}{\partial v} \frac{\partial L}{\partial q}\right) +\dot\phi_0(c_k)\left(\phi_j(c_k) \frac{\partial}{\partial q}\frac{\partial L}{\partial v} +\frac{1}{h}\dot\phi_j(c_k) \frac{\partial}{\partial v}\frac{\partial L}{\partial v} \right)\right). \]
Member Function Documentation
◆ computeJacobian()
|
inline |
\[ J_{ij} = \frac{\partial F_i}{\partial q_j} \]
Member Data Documentation
◆ m_v_cur_q
|
protected |
\(\bar q_n\), de longueur T_N_STEPS+1. Used instead of m_q0 WHICH IS IGNORED
◆ m_v_prev_q
|
protected |
\(\bar q_{n-1}\), de longueur T_N_STEPS+1. Used instead of m_q0 WHICH IS IGNORED
The documentation for this class was generated from the following file:
- Geomi/src/Variational/GalerkinStepInternals.hpp
